Οι 7 γέφυρες του Καλίνινγκραντ

Είναι δυνατόν μία χώρα να είναι γεωγραφικά χωρισμένη στα δύο; Είναι δυνατόν αυτά τα δύο μέρη να είναι εντελώς άνισα; Η απάντηση στις παραπάνω ερωτήσεις είναι καταφατική. Αν παρατηρήσει κανείς πολύ προσεκτικά τον χάρτη της σημερινής Ρωσίας, ανακαλύπτει ότι υπάρχει ένα γιγαντιαίο κομμάτι γης, που όλοι γνωρίζουμε και εκτείνεται από την Βαλτική και την Φινλανδία μέχρι τον Ειρηνικό ωκεανό, αλλά υπάρχει και ένα κομμάτι πολύ μικρό, αποκομμένο από την μεγαλύτερη ενιαία κρατική οντότητα στη γη σήμερα, το οποίο είναι και αυτό Ρωσικό έδαφος και στο οποίο εμπεριέχεται η ξακουστή πόλη Καλίνινγκραντ. Kaliningrad είναι το σύγχρονο όνομα της γνωστής πόλης Königsberg, γενέτειρας του γερμανού φιλόσοφου Immanuel Kant και του γερμανού μαθηματικού και στοχαστή David Hilbert. Στο ψυχρό και απομονωμένο Kaliningrad λοιπόν, άρχισε να ξετυλίγεται ο μίτος ενός νέου κεφαλαίου των μαθηματικών, που σήμερα χαρακτηρίζεται από τον όρο τοπολογία.

Η θέση του Καλίνινγκραντ  (από wkipedia.com)

Μία πόλη συγκέντρωσης λαμπρών εγκεφάλων

Κατά τη διάρκεια του 18ου αιώνα, όταν το Königsberg ήταν μέρος της μεγάλης αυτοκρατορικής Ρωσίας, υπήρχαν 7 γέφυρες που διέσχιζαν τον ποταμό Pregel. Είχε γίνει μέρος του απογευματινού Κυριακάτικου περιπάτου των κατοίκων, η άσκηση, να δουν αν μπορούν να περάσουν όλες τις γέφυρες του ποταμού διασχίζοντάς κάθε μία μόνο μία φορά. Όσο όμως και να προσπαθούσαν, πάντα υπήρχε μία γέφυρα που δεν μπορούσαν να προσεγγίσουν. Ήταν όντως αδύνατο ή απλά δεν είχαν βρει τον τρόπο που θα τους επέτρεπε να τις διασχίσουν όλες;

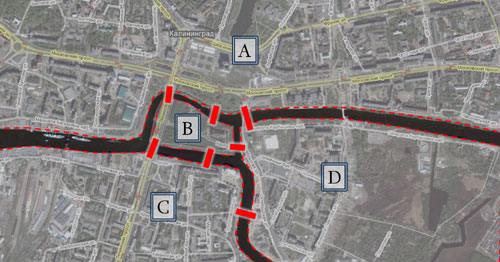
Χάρτης του Καλίνινγκραντ με τις γέφυρες και
τα κομμάτια γης που αυτές ενώνουν

Δεν ήταν μέχρι την άφιξη ενός Ελβετού μαθηματικού ονομαζόμενου Leonhard Euler – ο οποίος εφάρμοσε μία μαθηματική προσέγγιση στο πρόβλημα – που επιβεβαιώθηκε ότι το πρόβλημα ήταν αδύνατο να λυθεί: δεν υπήρχε δηλαδή τρόπος να διασχίσει κάποιος και τις 7 γέφυρες περνώντας κάθε μία μόνο μία φορά.

Ο Euler γεννήθηκε το 1707 στην Βασιλεία, όπου και το μαθηματικό ταλέντο του ανιχνεύτηκε από τους Bernoulli’s, μία πολύ σημαντική μαθηματική οικογένεια. Ο Euler πέρασε μεγάλο μέρος της μαθηματικής του ζωής στην ακαδημία της Αγ. Πετρούπολης και εκεί πρωτάκουσε για το περίεργο πρόβλημα των 7 γεφυρών του Königsberg.

Παλιό Ελβετικό χαρτονόμισμα με τον Euler

Το σημαντικό εννοιολογικό άλμα που πραγματοποίησε ο Euler, ήταν να συνειδητοποιήσει ότι οι πραγματικές διαστάσεις της πόλης δεν είχαν καμία σχέση με το πρόβλημα. Το πιο σημαντικό στοιχείο ήταν, το πώς συνδέονταν οι γέφυρες μεταξύ τους. Η ίδια αρχή διέπει για παράδειγμα και τον χάρτη του υπογείου του Λονδίνου: δεν είναι ένας ακριβής πραγματολογικά και φυσικά χάρτης, απλά περιέχει πληροφορίες για το πώς είναι συνδεδεμένοι οι σταθμοί. Όταν ο Euler σχεδίασε και ανέλυσε τον χάρτη του Königsberg με αυτό το τρόπο, συνειδητοποίησε ότι οι 4 περιοχές γης που συνδέονταν από τις γέφυρες, μπορούσαν να αντικατασταθούν από σημεία, ενώ οι γέφυρες από γραμμές που ένωναν τα σημεία. Το πρόβλημα λοιπόν του μοναδικού περιπάτου πάνω από όλες τις γέφυρες (και της μοναδικής λύσης στο πρόβλημα), ισοδυναμούσε με ένα πρόβλημα σχεδίασης στο χαρτί, μιας τελικής εικόνας-σχεδιαγράμματος, χωρίς να σηκωθεί το μολύβι από το χαρτί, αλλά και χωρίς να ζωγραφιστεί η ίδια γραμμή δύο φορές.

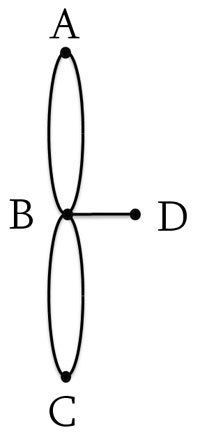
Η καινοτομία του Euler. Γραμμές και σημεία.

ΤΟ ΤΕΛΟΣ ΤΟΥ ΔΡΟΜΟΥ
Γιατί ήταν λοιπόν αδύνατο? O Euler συνειδητοποίησε ότι σε ένα γράφημα που το μονοπάτι θα ήταν εφικτό, κάθε σημείο που θα επισκεπτόταν το μολύβι θα έπρεπε να είχε μία γραμμή να καταλήγει και μία να ξεκινάει από αυτό. Εάν επισκεπτόσουν αυτό το σημείο ξανά, θα έπρεπε να υπάρχει μία καινούργια γέφυρα προς αυτό και από αυτό. Έτσι θα έπρεπε να υπάρχουν μόνο ζυγοί αριθμοί γεφυρών που να ακουμπούν κάθε σημείο. Οι μόνες εξαιρέσεις αυτού κανόνα είναι η αρχή και το τέλος του μονοπατιού. Το σημείο εκκίνησης έχει μόνο μία γραμμή που ξεκινάει από αυτό και το σημείο τερματισμού μία γραμμή που καταλήγει σε αυτό. Έτσι για να είναι ένα μονοπάτι εφικτό, όχι παραπάνω από δύο σημεία – η αρχή και το τέλος – πρέπει να έχουν μονό αριθμό γραμμών. Αν όμως δούμε την κάτοψη των 7 γεφυρών του Königsberg, κάθε σημείο έχει μονό αριθμό γεφυρών που ξεπηδούν από αυτό. Για αυτό και το εν λόγω ταξίδι ήταν αδύνατο να πραγματοποιηθεί.

Είναι ενδιαφέρον να δούμε σήμερα πόσες από τις γέφυρες εκείνες είναι ακόμα εκεί. Σαν ένα σημαντικό σημείο της Βαλτικής, η πόλη του Königsberg, ήταν ένα στρατηγικό σημείο για το Γερμανικό στόλο κατά τη διάρκεια του 2ου παγκοσμίου πολέμου και για αυτό και υπέφερε από πολύ ισχυρούς βομβαρδισμούς από τους συμμάχους. Μεγάλο μέρος του ιστορικού ιστού της πόλης ισοπεδώθηκε, συμπεριλαμβανομένου και του ξακουστού πανεπιστημίου στο νησί στην καρδιά της πόλης όπου ο Kant και ο Hilbert ανδρώθηκαν ακαδημαϊκά. Οι γέφυρες όμως;

Τρεις από τις προπολεμικές γέφυρες είναι ακόμα εκεί: η «ξύλινη» γέφυρα (Holzbrücke), η «μελί» γέφυρα (Honigbrücke) και η «ψηλή» γέφυρα High (Hohebrücke). Δύο γέφυρες έχουν εξαφανιστεί εντελώς: η γέφυρα «σφαγίων» (Köttelbrücke) και η γέφυρα του «σιδερά» (Schmiedebrücke). Οι υπόλοιπες γέφυρες – η πράσινη γέφυρα (Grünebrücke) και η γέφυρα του «έμπορου» (Krämerbrücke) – είχαν ξαναχτιστεί μετά τον πόλεμο για να σηκώσουν μεγάλο μεταφορικό μέρος μέσα στην πόλη.

Η μαθηματική ανάλυση του Euler έδειξε ότι αν υπήρχαν ακριβώς δύο σημεία με ζυγό αριθμό γεφυρών, τότε ένα μονοπάτι θα ήταν σίγουρα εφικτό: ξεκινάς από ένα με ζυγό αριθμό και καταλήγεις στο άλλο.

Η ιστορία των γεφυρών του Königsberg είναι σαν ένα παραμύθι που όλοι οι μαθηματικοί, μηχανικοί και αρχιτέκτονες πρέπει να ακούσουν κάποια στιγμή. Είναι σημαντικό γιατί γέννησε ένα νέο τρόπο προσέγγισης του χώρου και της γεωμετρίας. Αντί να ενδιαφερόμαστε για τις διαστάσεις, τις αποστάσεις και τις γωνίες μεταξύ γεωμετρικών οντοτήτων, αυτή η νέα προοπτική εστίαζε στο πως είναι συνδεδεμένες αυτές οι οντότητες. Αυτή ήταν και η αρχή της τοπολογίας, ενός από τα πιο ισχυρά παρακλάδια της μαθηματικής επιστήμης που μελετήθηκε τον τελευταίο αιώνα.
Αυτή η εξέλιξη οδήγησε ένα άφαντο μαθηματικό, κρυμμένο σε ένα σπίτι στην άκρη της Αγ. Πετρούπολης, να λύσει ένα από τα μεγαλύτερα αινίγματα της μαθηματικής τοπολογίας, την «εικασία του Poincare» .

Του Σίμου Γερασιμίδη

Αναφορές:
• BBC History Magazine, October, 2008
• www.wikipedia.com