ΤΕΧΝΙΚΟΣ ΚΟΣΜΟΣ
ΤΕΧΝΙΚΑ ΘΕΜΑΤΑ

14 Μάιος, 2008
Ο τέλειος πρόβολος – το πρόβλημα του Γαλιλαίου
Η αναζήτηση τέλειων μορφών γεωμετρίας, αναπόφευκτα οδηγεί την στήλη αυτή, στην μελέτη άλλης μίας φαινομενικά απλής στατικής λειτουργίας και κατασκευής όπως ο πρόβολος.
Του Σίμου Γερασιμίδη
Ένας Γαλιλαίος κάθε 2000 χρόνια, φτάνει.
Pius XII, Πάπας (1938-1958)

Ο πολύ μεγάλος πρόβολος στον πανέμορφο θόλο του Oscar Niemeyer στην Brazilia της Βραζιλίας.
Φωτογραφία του συγγραφέα.
Από τους πρώτους μελετητές, ιστορικά, που ασχολήθηκε με το πρόβλημα του προβόλου ήταν ο Γαλιλαίος στο βιβλίο του «Διάλογοι σχετικά με δύο καινούργιες επιστήμες». Εδώ είναι ευκαιρία να γραφτούν μερικά πράγματα για αυτό το βιβλίο που είναι μνημειώδες στην ιστορία της επιστήμης και της επιστημονικής σκέψης γενικά.

Το εξώφυλλο της αυθεντικής έκδοσης του έργου του Γαλιλαίου.
Από Two new Sciences by Galileo, New York, The Macmillan Company, 1914.
Το βιβλίο αυτό εκδόθηκε σε μία ανθούσα εκείνη την εποχή πόλη της Ολλανδίας, το Leyden, όταν ο Γαλιλαίος ήταν 74 χρονών. Πέντε χρόνια πριν, είχε καταδικαστεί ως αιρετικός με ισόβια φυλάκιση και του είχε απαγορευτεί επίσης να εκδώσει οποιοδήποτε βιβλίο. Όλα αυτά βέβαια στην Ρώμη. Η Ολλανδία ήταν εκτός της επιρροής της Ιεράς Εξέτασης και έτσι ο πασίγνωστος εκδοτικός οίκος Elseviers (υπάρχει μέχρι σήμερα) δέχθηκε να εκδώσει το βιβλίο.
Το βιβλίο είναι σε μορφή τεσσάρων διαλόγων (ένας πέμπτος προστέθηκε αργότερα). Οι τρεις συνομιλητές είναι ο Salviati, ο οποίος εκπροσωπεί τον Γαλιλαίο• ο Sagredo, ο οποίος εκπροσωπεί τον Γαλιλαίο σε νεότερη ηλικία έχοντας ιδέες που σποραδικά εκφράζει και τις οποίες ο ηλικιωμένος Γαλιλαίος απορρίπτει ή έχει ήδη απορρίψει• και ο Simplicio, ο οποίος μάλλον αντιπροσωπεύει ένα πολύ νέο Γαλιλαίο και ο οποίος λειτουργεί πολλές φορές σαν κόλακας των άλλων δύο μορφωμένων και έξυπνων συνομιλητών του.
Ο κάθε διάλογος υποτίθεται ότι διαρκεί μία ημέρα. Ο τρίτος και ο τέταρτος διάλογος αφορούν την «δημιουργία» της επιστήμης της μηχανικής (προ-Νευτωνιακής)• είναι ο δεύτερος διάλογος (η δεύτερη ημέρα) στον οποίο ο Γαλιλαίος ασχολείται με θέματα γεωμετρίας των κατασκευών.
Το βιβλίο βέβαια περιέχει και πολύ σημαντικές διαπιστώσεις και έρευνες της εποχής, όπως για παράδειγμα στον πρώτο διάλογο όπου προκύπτει η ιδέα ότι σε ένα πεπερασμένο χώρο μπορεί να περιλαμβάνονται άπειρος αριθμός κενών. Είναι από τις πρώτες φορές που μπαίνουν ζητήματα απειροστικού λογισμού. Ή ακόμα, είναι αυτό το βιβλίο στο οποίο ο Γαλιλαίος περιγράφει για πρώτη φορά τον διαβόητο ισχυρισμό του ότι δύο αντικείμενα με διαφορετικό βάρος πέφτουν (μέσα στο πεδίο βαρύτητας) με την ίδια ταχύτητα προς την γη αν αφεθούν από το ίδιο ύψος.
Φτάνοντας όμως στο τέλος της δεύτερης ημέρας προκύπτει το ενδιαφέρον για εμάς πρόβλημα. Το πρόβλημα του τέλειου σχήματος ενός προβόλου. Του σχήματος εκείνου που είναι ίσης αντοχής, δηλαδή του σχήματος που θα αστοχήσει ταυτόχρονα σε όλες τις διατομές του αν φορτιστεί με ένα μοναχικό φορτίο στην άκρη του.

Σκίτσο από την αυθεντική έκδοση του Γαλιλαίου. Πρόβολος με μοναχικό φορτίο στην άκρη.
Από Two new Sciences by Galileo, New York, The Macmillan Company, 1914.
Ένας οποιοσδήποτε πρόβολος σταθερής διατομής κατά μήκος, με ένα μοναχικό φορτίο στην άκρη του, αστοχεί μόνο στην βάση (ΑΒ). Αυτή είναι η κρίσιμη διατομή. Αν όμως ο ίδιος πρόβολος κοπεί στην διαγώνιό του (βλέπε σχήμα, επίπεδο BFD) με αποτέλεσμα να γίνει μεταβλητής διατομής, γίνεται αμέσως πιο ασθενής και τελικά μία τυχαία διατομή CN είναι αυτή που αστοχεί από την ροπή κάμψης και όχι η βάση του. Το φορτίο δεν μπορεί να ακολουθήσει την πορεία που είχε προηγουμένως και δεν μεταφέρεται στην βάση του.
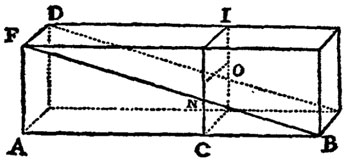
Σκίτσο από την αυθεντική έκδοση του Γαλιλαίου. Πρόβολος κομμένος στην διαγώνιό του.
Από Two new Sciences by Galileo, New York, The Macmillan Company, 1914.
Θα πρέπει να υπάρχει μία γεωμετρία η οποία να μεταβάλλει τη διατομή του προβόλου κατά μήκος του και να είναι κάθε φορά η απαιτούμενη για να ανταπεξέλθει στα φορτία διατομής του συγκεκριμένου σημείου. Ο Γαλιλαίος αποδεικνύει ότι ένας πρόβολος, σταθερού πλάτους, πρέπει να έχει ύψος διατομής το οποίο να μεταβάλλεται σύμφωνα με το τετράγωνο της απόστασης από την άκρη και αυτό αποτελεί σύμφωνα με τον Salviati μία παραβολή με κορυφή το σημείο Β. Είναι η πρώτη προσέγγιση της ροπής αδράνειας όπως την γνωρίζουμε σήμερα. Σήμερα γνωρίζουμε ότι η ροπή αδράνειας που αφορά την αντοχή της διατομής μας σε ροπή κάμψης είναι συνάρτηση δευτέρου βαθμού ως προς το ύψος της διατομής (φυσικά πάντα για ορθογωνικές διατομές).
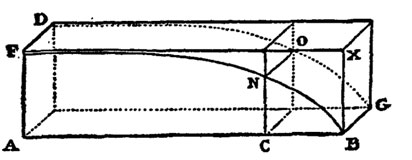
Σκίτσο από την αυθεντική έκδοση του Γαλιλαίου. Πρόβολος κομμένος με παραβολή.
Από Two new Sciences by Galileo, New York, The Macmillan Company, 1914.
Αναφορές:
1. The online library of Liberty, http://oll.libertyfund.org/index.php?option=com_frontpage&Itemid=149
2. Galileo Galilei, Two new Sciences by Galileo, translation from Henry Crew and Alfonso de Salvio, New York, The Macmillan Company, 1914.
3. Structural Analysis, Jacques Heyman, Cambridge University Press, 1998.
4. http://www.elsevier.de








