Η φωλιά του πουλιού

«Η μάθηση χωρίς την σκέψη είναι χαμένος κόπος. Η σκέψη χωρίς την μάθηση είναι απόγνωση.»

Κομφούκιος, Στοίχος 15, Κεφάλαιο Δεύτερο, Lun Yu

Η κινέζικη μυθολογία, όπως και η Ελληνική, είναι ατελείωτη και λεπτομερέστατη. Μέσα στο χάος και στο μεγαλείο της απειρότητάς της εμφανίζεται ένας ήρωας, με το όνομα Shen I, ο οποίος έχοντας ανθρώπινες και θεϊκές ιδιότητες ακολουθεί ένα δρόμο, μια άλλη Οδύσσεια, με σκοπό την εξήγηση φυσικών φαινομένων και την ανακάλυψη νέων κόσμων πραγματικών και μη. Είναι εντυπωσιακό ότι ο χαρακτήρας αυτός αναφέρεται συχνά σαν ο καλύτερος αρχιτέκτονας και ο ικανότερος μηχανικός, πράγμα που τον κάνει ιδιαίτερα έμπιστο για τους Θεούς και τους αυτοκράτορες αναλαμβάνοντας συνεχώς να διεκπεραιώνει αποστολές που του ανατίθενται. Σε κάποιο σημείο της περιπέτειάς του, στην πορεία προς το παλάτι του ήλιου και αφού έχει ήδη σκοτώσει τους εννέα ψεύτικους ήλιους, συναντά τον Θεό των αθανάτων και ακούει συμβουλές σχετικά με το φαινόμενο της ημέρας και της νύχτας.

«Ο ήλιος ανατέλλει και δύει σε συγκεκριμένους χρόνους· δεν ξέρεις όμως ακόμα τους κανόνες της ημέρας και της νύχτας· σου είναι απολύτως αναγκαίο να πάρεις μαζί σου το πουλί με το χρυσό φτέρωμα, που θα σου τραγουδήσει για να σε συμβουλέψει ποιες ακριβώς είναι οι στιγμές της ανατολής, του ζενίθ και της δύσης του ήλιου. Ο Shen I απαντάει, που θα βρω το πουλί αυτό? Και ο Θεός τον συμβουλεύει ξανά: Είναι αυτό που θα ακούσεις να φωνάζει Ια!Ια! Είναι ο πρόγονος της πνευματικότητας της αρσενικής αρχής. Έχοντας καταπιεί την ενεργή αξία του ήλιου, έχει πάρει την μορφή ενός τρίποδου πουλιού, που έχει κάνει φωλιά στο δέντρο fusang στο κέντρο της Ανατολικής Θάλασσας. Αυτό το δέντρο είναι αρκετά χιλιάδες μέτρα ψηλό και έχει γιγαντιαία περιφέρεια. Το πουλί περιμένει κοντά στο ξεκίνημα της ανατολής και μόλις δει τον ήλιο να κάνει το πρωινό του μπάνιο, ξεσπά σε ένα κλάμα που ταρακουνάει τους παράδεισους και ξυπνά όλη την ανθρωπότητα.»

Σήμερα, μπορεί η φωλιά του πουλιού να μην είναι σε ύψος χιλιομέτρων, είναι όμως σίγουρα γιγαντιαίας περιφέρειας. Η σύγχρονη Κίνα μπορεί να καυχιέται ότι έφτιαξε επιτέλους την φωλιά για να στεγάσει το μυθολογικό πουλί που έμενε κάπου σε μια Ανατολική Θάλασσα, σε ένα πανύψηλο δέντρο. Πλέον η «φωλιά του πουλιού», βρίσκεται στο Πεκίνο, είναι έτοιμη, πολύπλοκη, χαοτική αλλά πάνω απ’ όλα πραγματική.

Render από http://wirednewyork.com/forum/showthread.php?t=3756

Γεωμετρία
Πολύπλοκες επιφάνειες και γεωμετρίες έχουν προσελκύσει την προσοχή και είναι πολύ δημοφιλείς στο πεδίο της σύγχρονης αρχιτεκτονικής. Αντίθετα με τον μινιμαλισμό της μοντέρνας αρχιτεκτονικής, οι πολυπλοκότητες της σύγχρονης πρακτικής ενεργοποιούν αξίες ποικιλότητας, πλούτου και χωρικής κατανόησης μέσα από πολυπρόσωπες φόρμες. Παρόλο που αυτές οι γεωμετρίες υποθέτουν ένα επίπεδο χάους, οι πολυπλοκότητες είναι αρκετά ακριβείς στην μεθοδολογία τους. Στην διαδικασία εφαρμογής αυτών των ψηφιακών σχημάτων στην πραγματικότητα, μία συστηματική μεθοδολογία πρέπει να στοιχειοθετηθεί, ώστε να υπάρξει στατική επιτυχία. Μέσα από το Ολυμπιακό Στάδιο του Πεκίνου, απλές ιδέες ξεκίνησαν αυτήν την επικοινωνιακή ιδεολογία.

Η γεωμετρία της στέγης του Ολυμπιακού Σταδίου του Πεκίνου με μια πρώτη ματιά μοιάζει πολύπλοκη, αλλά στην πραγματικότητα βασίζεται σε μία λογική που βήμα προς βήμα σχεδιάζει και συνθέτει απλά γεωμετρικά σχήματα. Η στέγη περικλείεται κυρίως από δύο ελλείψεις (σχήμα 1). Η πρώτη, η μεγάλη εξωτερική έλλειψη (ακτινών 266μ και 312μ) αποτελεί το εξωτερικό σύνορο της στέγης, ενώ η εσωτερική έλλειψη (ακτινών 74μ και 40μ) διαιρεμένη στην μέση από ένα ευθύγραμμο παραλληλόγραμμο διαστάσεων 74x94μ δημιουργεί μία μεγάλη οπή στο κέντρο της οροφής. Πρέπει εδώ να σημειωθεί ότι το άνοιγμα αυτό είχε αρχικά σχεδιαστεί να καλύπτεται από μία πτυσσόμενη οροφή, αλλά για διάφορους λόγους, η λύση αυτή τελικά απορρίφθηκε.

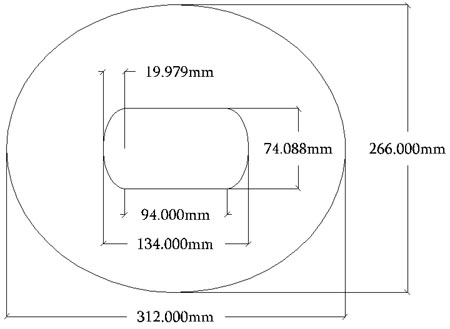
Σχήμα 1, από Innovations in structures, Harvard University Graduate School of Design, 2006

Το επόμενο βήμα προς την κατανόηση της γεωμετρίας της στέγης είναι να διαιρέσουμε την εξωτερική έλλειψη σε 24 ίσα τμήματα, τα άκρα των οποίων και αποτελούν τα σημεία που τοποθετούνται οι 24 βασικές κολώνες που μεταφέρουν τα φορτία στο έδαφος. Από αυτά τα σημεία, που βρίσκονται στην εξωτερική έλλειψη, είναι πολύ εύκολο και απλό να σχεδιαστούν οι εφαπτόμενες (δύο για κάθε σημείο) προς την εσωτερική έλλειψη (σχήμα 2).

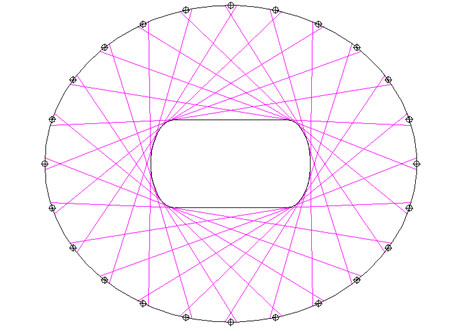
Σχήμα 2, από Innovations in structures, Harvard University Graduate School of Design, 2006

Το γεωμετρικό σύνολο που δημιουργείται, αποτελείται ουσιαστικά από 12 τεράστια πλαίσια που συναντώνται στη μέση του ανοίγματός τους, ακριβώς πάνω στην εσωτερική έλλειψη και επίσης συνδέονται σε όλα τα σημεία που τέμνονται μεταξύ τους. Η στατική διάταξη των 12 πλαισίων δημιουργεί ένα εξαιρετικά άκαμπτο και απαραμόρφωτο φορέα που λειτουργεί πολύ αποτελεσματικά σαν διάφραγμα στο επίπεδο της οροφής.

Για το Στάδιο, η πολυπλοκότητα δημιουργείται από διάφορα δευτερεύοντα στατικά συστήματα που υπάρχουν και λειτουργούν πάνω στο κύριο σύστημα των 12 πλαισίων, προσθέτοντας μεν αρκετή δυσκαμψία αποφεύγοντας δε ταυτόχρονα να βαραίνουν τον φορέα.
Το πρώτο και πιο απλό από τα δευτερεύοντα συστήματα (φαίνεται με πράσινο χρώμα στο σχήμα 3), παράγεται ενώνοντας ένα σύνολο σημείων τομής ανά δύο κυρίων πλαισίων (μία σειρά πράσινων σημείων ενωμένα με μία πράσινη καμπύλη), με το μέσο ενός συγκεκριμένου τμήματος των κυρίων πλαισίων όπως φαίνεται στο σχήμα 3 (μια σειρά κόκκινων σημείων).

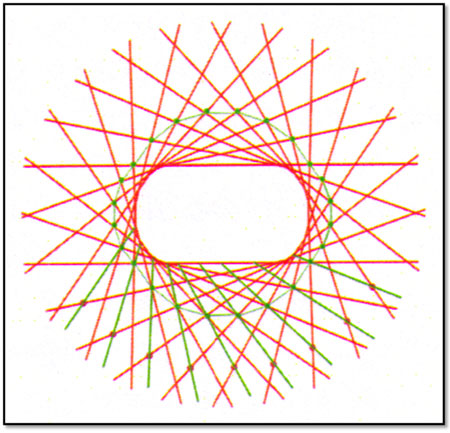
Σχήμα 3, από Innovations in structures, Harvard University Graduate School of Design, 2006,
(CATIA Junfeng Ding, Qiuda Lin)

Ένα επιπλέον επίπεδο δευτερευόντων δικτυωμάτων (φαίνεται με σιέλ στο σχήμα 4), παράγεται ενώνοντας ένα άλλο σύνολο σημείων τομής ανά δύο κυρίων πλαισίων, (μια σειρά μπλε σημείων), με το σημείο τομής των πράσινων δευτερευόντων δικτυωμάτων με τα κύρια-κόκκινα (μια σειρά σιέλ σημείων).

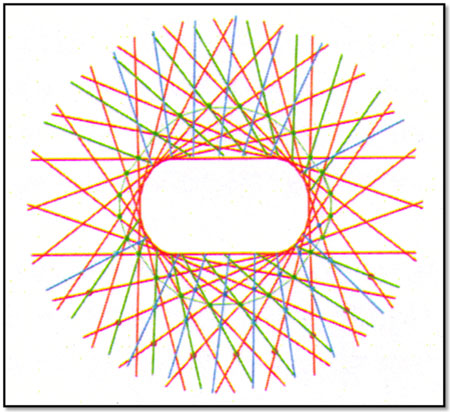
Σχήμα 4, από Innovations in structures, Harvard University Graduate School of Design, 2006,
(CATIA Junfeng Ding, Qiuda Lin)

Για την ενίσχυση της δυσκαμψίας του στατικού συστήματος, ένα τρίτο σύστημα, το πολυγωνικό σύστημα, προστίθεται πάνω στα κύρια και τα δευτερεύοντα δικτυώματα. Ακολουθώντας κάποιους αντίστοιχους συγκεκριμένους κανόνες, το πολυγωνικό σύστημα πλαισιώνεται με ορισμένα σκούρα κίτρινα, καφέ, ανοιχτά κίτρινα δικτυώματα, προσθέτοντας ακόμη παραπάνω οπτικό χάος στο σύνολο της κατασκευής (σχήμα 5).

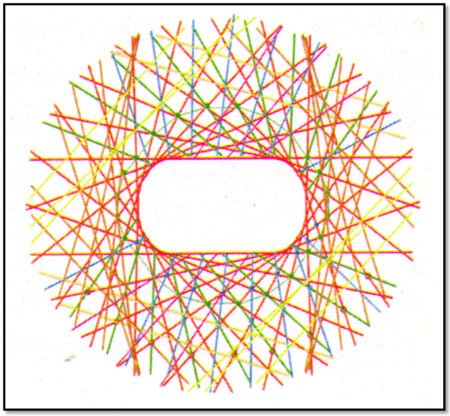
Σχήμα 5, από Innovations in structures, Harvard University Graduate School of Design, 2006,
(CATIA Junfeng Ding, Qiuda Lin)

Το αποτέλεσμα όλων των παραπάνω συνθέτουν την φαινομενικά χαοτική γεωμετρία του Σταδίου σε κάτοψη. Παρόλα αυτά η πολυπλοκότητα της γεωμετρίας της οροφής δεν εξαντλείται μόνο στο επίπεδο της, μιας και δεν είναι επίπεδη, αλλά εμφανίζει κάθετα στο επίπεδό της μία διπλή καμπυλότητα. Με μία πρόχειρη σχεδίαση όλων των παραπάνω (σε απλουστευτική μορφή και κρατώντας μόνο το κύριο στατικό σύστημα) καταλήγουμε στην παρακάτω γεωμετρία.

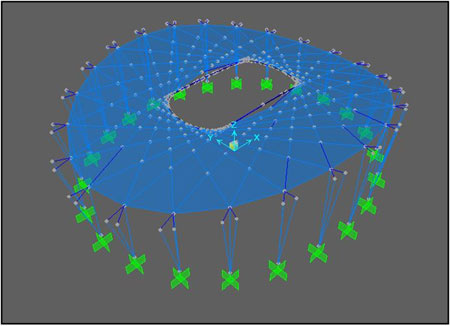
3D όψη του μοντέλου του Σταδίου, Simos Gerasimidis, Jeremiah O’Neill

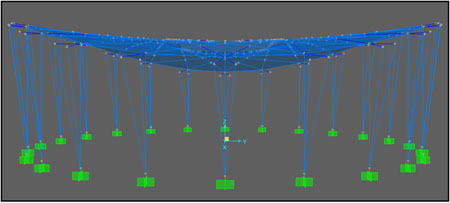
Θετική καμπυλότητα του Σταδίου στην μικρή διεύθυνση,
Simos Gerasimidis, Jeremiah O’Neill

Αρνητική καμπυλότητα του Σταδίου στην μεγάλη διεύθυνση,
Simos Gerasimidis, Jeremiah O’Neill

Σε αυτό το σημείο πρέπει να δοθεί ξεχωριστή προσοχή στο σύστημα με το οποίο είναι σχεδιασμένες οι κολώνες του σταδίου. Οι 24 βασικές κολώνες απαρτίζονται από 3 διαφορετικά και ανεξάρτητα στοιχεία που καταλήγουν στο έδαφος στο ίδιο σημείο, έχουν όμως διαφορετική στατική λειτουργία (σχήμα). Η κατάληξη 2 πλαισίων διαφορετικού επιπέδου στην ίδια κολώνα, δημιουργεί ένα πρόβλημα σύγκλισης που μπορεί να λυθεί περιλαμβάνοντας 3 διαφορετικά στοιχεία στην ίδια κολώνα. Όπως φαίνεται στο σχήμα το κάθε στοιχείο τοποθετείται αναλόγως για να υποδεχθεί το πλαίσιο που καταλήγει σε αυτό.

 Από την ανάλυση προκύπτει πολύ εύκολα ότι το στοιχείο που είναι στην εσωτερική πλευρά του σταδίου είναι σε θλίψη ενώ τα δύο υπόλοιπα στοιχεία είναι σε εφελκυσμό (υπό το ίδιο βάρος της κατασκευής).

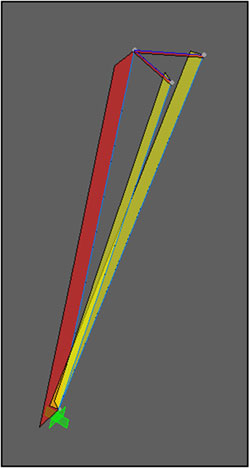
Στατική λειτουργία κολώνας,
Simos Gerasimidis, Jeremiah O’Neill

Για να τσεκάρουμε αν πραγματικά το στάδιο συμπεριφέρεται όπως έχει σχεδιαστεί, δηλαδή σαν μία σειρά από πλαίσια κάναμε τον εξής έλεγχο. Απομονώσαμε ένα πλαίσιο και είδαμε πως συμπεριφέρεται, δηλαδή είδαμε τα φορτία διατομής υπό μόνιμη φόρτιση. Είναι αξιοσημείωτο ότι το διάγραμμα ροπών του πλαισίου αυτού είναι ακριβώς ίδιο με το διάγραμμα ροπών ενός τυπικού πλαισίου κάτω από ομοιόμορφη, μόνιμη φόρτιση. Αυτό αποδεικνύει ότι η οροφή του Σταδίου λειτουργεί πραγματικά σαν μία αλληλουχία πλαισιωτών φορέων που είναι τοποθετημένα το ένα δίπλα στο άλλο. Η χαοτική όψη δηλαδή μιας τέτοιας κατασκευής, απλουστευτικά καταλήγει στην απλή και ευκολονόητη λειτουργία πλαισίου.

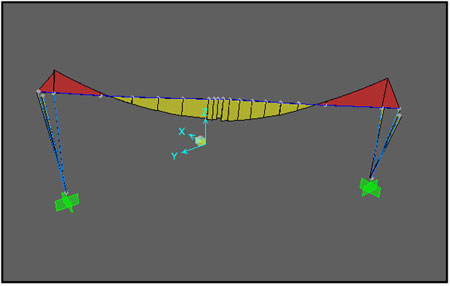
Στατική λειτουργία πλαισίου, Simos Gerasimidis, Jeremiah O’Neill

Του Σίμου Γερασιμίδη

Αναφορές:
1. Μyths and Legends of China, E.T.C. Werner, 2005,
http://www.gutenberg.org/files/15250/15250-h/15250-h.htm#d0e1278
2. http://wirednewyork.com/forum/showthread.php?t=3756
3. Innovations in structures, Harvard University Graduate School of Design, 2006