Το πρόβλημα του περιπλανώμενου εμποράκου (Α΄μέρος)

«Στο βουνό ο συντομότερος δρόμος είναι από κορφή σε κορφή: μα για κάτι τέτοιο πρέπει να’ χεις μακριά ποδάρια. Τα γνωμικά πρέπει να είναι κορφές: και αυτοί, που για αυτούς προορίζονται, πρέπει να είναι μεγάλοι και να’ χουν το ίδιο ανάστημα.»

Φρειδερίκος Νίτσε, Τάδε Έφη Ζαρατούστρα

"In the mountains the shortest route is from peak to peak, but for that you must have long legs. Aphorisms should be peaks; and those to whom they are spoken should be big and tall of stature."

Friedrich Nietzsche, Also Sprach Zarathustra

Καλοκαίρι και οι περισσότεροι κάτω από τις ομπρέλες απολαμβάνουμε κάποιο βιβλίο στην ησυχία της παραλίας ή εναλλακτικά κρατάμε ένα περιοδικό με σταυρόλεξα προσπαθώντας να προκαλέσουμε την δύναμη της μνήμης μας. Συνήθως στις σελίδες τέτοιων περιοδικών βρίσκεται και πληθώρα διαφορετικών γρίφων με σκοπό να περάσουμε με ενδιαφέρον την ώρα μας. Ανέκαθεν, ένα από τα πιο περίεργα και άσχετα με το θέμα των περιοδικών παιχνίδια, είναι εκείνος ο παιδικός γρίφος, στον οποίο πρέπει να ενώσουμε τις τελείες για να προκύψει ένα σχήμα/σκίτσο, με την προϋπόθεση το μολύβι μας να μην περάσει από την ίδια τελεία δύο φορές. Πως όμως έχει προκύψει αυτό το παιχνίδι;

Παιδικό παιχνίδι με τελείες

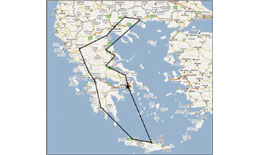
Πίσω από αυτό το παιχνίδι/πρόβλημα κρύβεται μία ολόκληρη μαθηματική θεωρία που σήμερα εφαρμόζεται σε πολλές επιστήμες προσπαθώντας να βελτιστοποιήσει μία μεταβλητή μιας συνάρτησης. Δεν είναι καθόλου τυχαίο ότι με αυτό το πρόβλημα έχουν ασχοληθεί μεγάλοι μαθηματικοί με τις ερευνητικές τους ομάδες και μεγάλα πανεπιστήμια, αφιερώνοντας μεγάλα ερευνητικά προγράμματα χωρίς να μπορέσουν να βρουν μέχρι σήμερα την ακριβή λύση στο πρόβλημα. Με μία πρώτη ματιά μπορεί να φαίνεται ένα ασήμαντο και απλό ερώτημα, δεν είναι όμως ακριβώς έτσι. Αρκεί να διατυπωθεί το πρόβλημα αλλιώς· ας υποθέσουμε ότι ένας έμπορος στην διαδικασία να προωθήσει τα προϊόντα του πρέπει να επισκεφτεί τις 15 μεγαλύτερες πόλεις της Ελλάδας και για αυτό το λόγο προσπαθεί να βρει την συντομότερη διαδρομή ανάμεσα σε αυτές τις πόλεις. Ποιος είναι ο τρόπος (αλγόριθμος) που πρέπει να εφαρμόσει;

Χάρτης της Ελλάδας με τις 15 μεγαλύτερες πόλεις (απογραφή 2001)

Το πρόβλημα του περιπλανώμενου εμποράκου είναι ένα πρόβλημα συνδυαστικής βελτιστοποίησης που μελετάται στην θεωρητική επιστήμη των υπολογιστών και στην έρευνα εφαρμογών. Με δεδομένη μία λίστα από πόλεις και των μεταξύ τους αποστάσεων, το ζητούμενο του προβλήματος είναι να βρεθεί η συντομότερη διαδρομή που θα περιλαμβάνει όλες τις πόλεις από μία μόνο φορά.

Το πρόβλημα αρχικά διατυπώθηκε σαν ένα μαθηματικό πρόβλημα το 1930 και είναι ένα από τα πιο εντατικά μελετημένα προβλήματα βελτιστοποίησης με αποτέλεσμα να θεωρείται σημείο αναφοράς για πολλές μεθόδους βελτιστοποίησης. Παρόλη τη μαθηματική δυσκολία του προβλήματος, ένας μεγάλος αριθμός εμπειρικών αλλά και επακριβών μεθόδων είναι γνωστός και έτσι προβλήματα που περιλαμβάνουν δεκάδες χιλιάδες πόλεις μπορούν να λυθούν.

Το πρόβλημα του περιπλανώμενου εμποράκου έχει πληθώρα εφαρμογών ακόμη και στην πιο αρχική διατύπωση, όπως στον σχεδιασμό, στην λογιστική και στην κατασκευή μικροτσίπ. Με λίγες αλλαγές, εμφανίζεται σαν ένα υπο-πρόβλημα πολλών τομέων όπως για παράδειγμα της γενετικής αλληλουχίας. Σε αυτές τις εφαρμογές, η έννοια της πόλης αντιστοιχεί για παράδειγμα σε πελάτες ή κομμάτια DNA  και η έννοια απόσταση αντιστοιχεί σε χρόνο ταξιδιού ή κόστος ή σε ομοιότητες μεταξύ κομματιών DNA. Σε πολλές εφαρμογές, επιπλέον περιορισμοί όπως περιορισμένοι πόροι ή παράθυρα χρόνου καθιστούν το πρόβλημα ακόμη δυσκολότερο.

Στην θεωρία της υπολογιστικής πολυπλοκότητας, η εκδοχή του προβλήματος του περιπλανώμενου εμποράκου ανήκει στην κλάση των NP-problems, δηλαδή nondeterministic polynomial time problems. Τα προβλήματα αυτά χαρακτηρίζονται κυρίως από την εξής ιδιότητά τους:

Παρόλο που οποιαδήποτε λύση στο πρόβλημα μπορεί να επαληθευτεί πολύ γρήγορα, δεν υπάρχει κανένας γνωστός τρόπος για να βρεθεί μία λύση. Το πιο χαρακτηριστικό γνώρισμα των NP-problems είναι ότι καμία γρήγορη λύση δεν είναι γνωστή. Άρα, ο χρόνος που απαιτείται για να λυθεί ένα πρόβλημα χρησιμοποιώντας οποιοδήποτε γνωστό αλγόριθμο αυξάνεται πολύ γρήγορα όσο το μέγεθος του προβλήματος αυξάνεται, με αποτέλεσμα ο χρόνος που χρειάζεται για να λυθούν ακόμη και μεσαία προς μεγάλα προβλήματα να είναι στο επίπεδο των εκατομμυρίων ή δισεκατομμυρίων χρόνων, χρησιμοποιώντας την υπολογιστική δύναμη που είναι διαθέσιμη σήμερα. Αυτό έχει ως συνέπεια, ότι  μόνο και ο καθορισμός αν είναι δυνατόν να λυθεί το πρόβλημα ή όχι να είναι από τα κύρια άλυτα προβλήματα στην επιστήμη των ηλεκτρονικών υπολογιστών.

ΙΣΤΟΡΙΑ
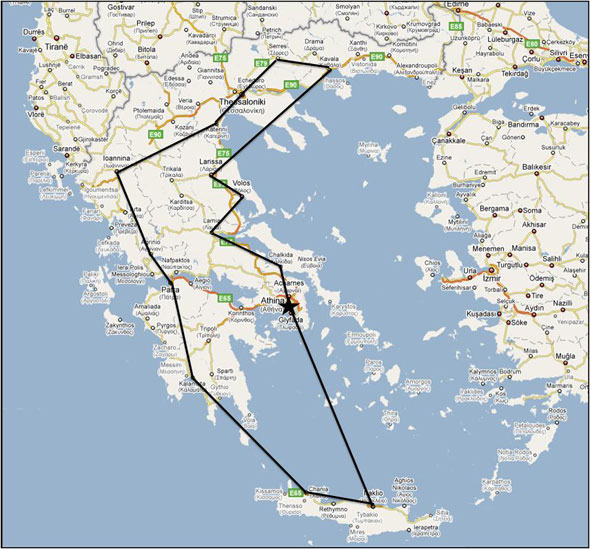
Η πηγή του προβλήματος του περιπλανώμενου εμποράκου είναι ασαφής. Ένα εγχειρίδιο για περιπλανώμενους εμπόρους του 1832 αναφέρει το πρόβλημα και περιλαμβάνει παραδείγματα διαδρομών μέσα στη Γερμανία και την Ελβετία, αλλά δεν περιέχει καθόλου μαθηματική αντιμετώπιση.

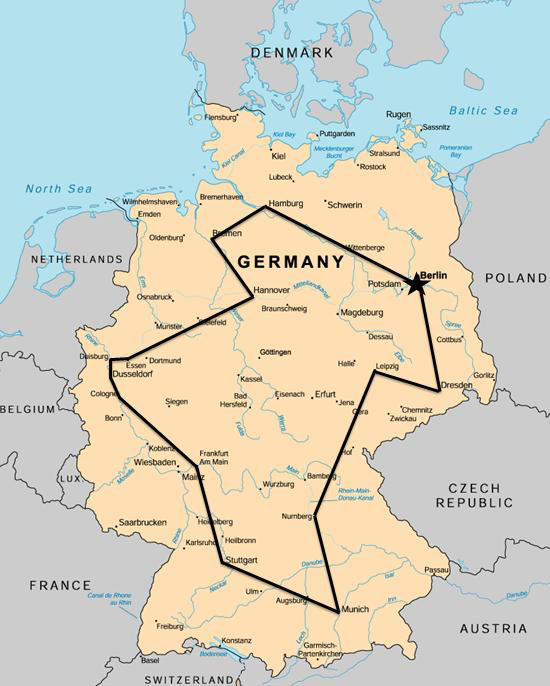
Χάρτης της Γερμανίας με τις 15 μεγαλύτερες πόλεις

Τα μαθηματικά προβλήματα σχετικά με τον περιπλανώμενο εμποράκο αντιμετωπίστηκαν για πρώτη φορά γύρω στα 1800 από τον Ιρλανδό μαθηματικό W.R. Hamilton και από τον Βρετανό μαθηματικό Thomas Kirkman. Το Icosian Game του Hamilton ήταν ένα ψυχαγωγικό παιχνίδι βασισμένο στον κύκλο του Hamilton. Η γενική μορφή του προβλήματος του περιπλανώμενου εμποράκου φαίνεται να πρωτοαναλύθηκε από μαθηματικούς γύρω στα 1930 στην Βιέννη και στο Harvard, από τον Karl Menger, ο οποίος καθορίζει το πρόβλημα, λαμβάνει υπόψη τον προφανή αλγόριθμο brute-force και παρατηρεί ότι η εμπειρική προσέγγιση του πλησιέστερου σημείου δεν αποκαλύπτει την βέλτιστη διαδρομή:

Καθορίζουμε ως πρόβλημα του αγγελιοφόρου (αφού πρακτικά το ίδιο πρόβλημα πρέπει να λυθεί από κάθε ταχυδρόμο, ή σε κάθε περίπτωση και από πολλούς ταξιδιώτες) το έργο να ευρεθεί, για ένα πεπερασμένο μεγάλο αριθμό σημείων των οποίων οι μεταξύ τους σε ζευγάρια, οι αποστάσεις είναι γνωστές, η συντομότερη διαδρομή που ενώνει τα σημεία. Φυσικά, το πρόβλημα είναι δυνατόν να λυθεί με πεπερασμένο αριθμό δοκιμών. Κανόνες που μπορούν να μειώσουν τις δοκιμές κάτω από τον αριθμό δυνατών συνδυασμών δεν είναι γνωστοί. Ο κανόνας ότι κάποιος πρέπει να πάει από την αφετηρία στο κοντινότερο σημείο και μετά στο κοντινότερο αυτού κ.ο.κ., δεν παράγει την συντομότερη διαδρομή.

Ο Hassler Whitney στο πανεπιστήμιο του Princeton αμέσως μετά εισήγαγε το όνομα «το πρόβλημα του περιπλανώμενου εμποράκου».

Γύρω στα 1950 και στα 1960 το πρόβλημα έγινε ιδιαίτερα δημοφιλές στους επιστημονικούς κύκλους της Ευρώπης και της Αμερικής. Σημαντικές συνεισφορές έγιναν από τους George Dantzig, Delbert Ray Fulkerson και Selmer M. Johnson στο RAND Corporation της Σάντα Μόνικα, οι οποίοι εξέφρασαν το πρόβλημα ως ένα γραμμικό πρόβλημα ακέραιων αριθμών και ανέπτυξαν την μέθοδο του τεμνόμενου επιπέδου (βλέπε επόμενα άρθρα της στήλης αμφίστυλο). Με αυτές τις νέες μεθόδους έλυσαν την περίπτωση με τις 49 πόλεις σε επίπεδο βέλτιστο, κατασκευάζοντας μία διαδρομή και αποδεικνύοντας ότι καμία άλλη δεν μπορεί να είναι συντομότερη. Στις επόμενες δεκαετίες, το πρόβλημα μελετήθηκε από πολλούς ερευνητές των μαθηματικών, της επιστήμης των υπολογιστών, της χημείας, της φυσικής αλλά και άλλων επιστημών.

Ο Richard M. Karp το 1972 έδειξε ότι ο κύκλος του Hamilton ήταν ένα πρόβλημα NP-complete που υποδούλωνε την δυσκολία NP και του προβλήματος του περιπλανώμενου εμποράκου. Αυτό προμήθευσε την επιστημονική εξήγηση για την επικείμενη υπολογιστική δυσκολία της εξεύρεσης των βέλτιστων διαδρομών.

Μεγάλη πρόοδος εμφανίστηκε στα τέλη της δεκαετίας του 1970 και 1980, όταν οι Grötschel, Padberg, Rinaldi και άλλοι κατάφεραν να λύσουν επακριβώς περιπτώσεις μέχρι και 2392 πόλεων, χρησιμοποιώντας μεθόδους τεμνόμενων επιπέδων και branch-and-bound methods.

Στα 1990, οι Applegate, Bixby, Chvátal, και Cook ανέπτυξαν το πρόγραμμα Concorde που χρησιμοποιείται σε πολλές πρόσφατες λύσεις. Ο Gerhard Reinelt εξέδωσε το 1991 το TSPLIB, μία συλλογή ενδεικτικών περιπτώσεων μεταβαλλόμενης δυσκολίας που χρησιμοποιήθηκε από πολλές ερευνητικές ομάδες για σύγκριση αποτελεσμάτων. Το 2005, ο Cook και άλλοι υπολόγισαν μία βέλτιστη διαδρομή μίας περίπτωσης του προβλήματος που είχε 33810 πόλεις δίνοντας μία διάταξη μικροτσίπ, η οποία μέχρι στιγμής είναι το μεγαλύτερο, σε αριθμό πόλεων, πρόβλημα περιπλανώμενου εμποράκου που έχει λυθεί. Για πολλές άλλες περιπτώσεις με εκατομμύρια πόλεις, λύσεις μπορούν να βρεθούν που είναι μέσα στο 1% από την βέλτιστη διαδρομή.

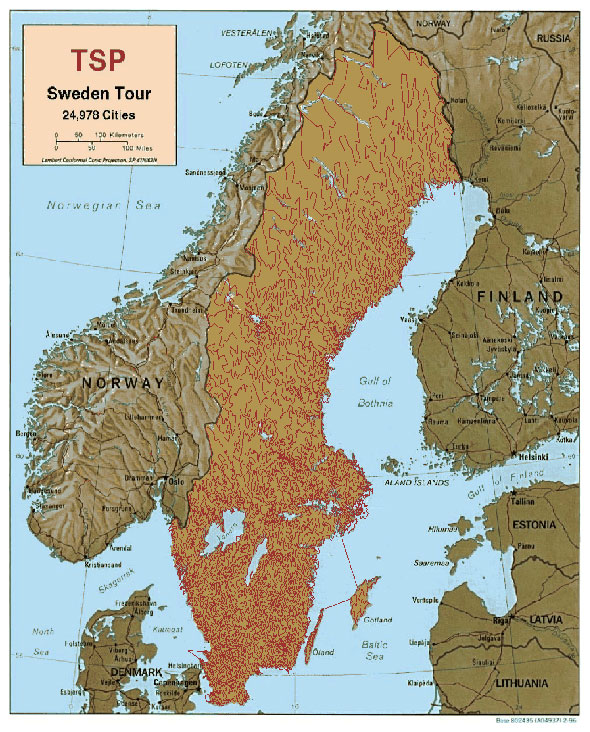
Η Σουηδία «λυμμένη» με 24978 πόλεις, το 2004, από τους Applegate, Bixby, Chvatal, Cook και Helsgaun

Τον Φεβρουάριο του 2009 ο Robert Bosch δημιούργησε ένα αντίστοιχο πρόβλημα περιπλανώμενου εμποράκου με θέμα την Μόνα Λίσα του Λεονάρντο Ντα Βίντσι, έχοντας 100.000 σαν σημεία/πόλεις, με σκοπό η λύση του να αποτελεί την δημιουργία του πίνακα σαν μια συνεχή γραμμή. Η βέλτιστη λύση για αυτό το πρόβλημα ακόμα είναι άγνωστη και όταν βρεθεί θα αποτελεί παγκόσμιο ρεκόρ λύσης προβλήματος περιπλανώμενου εμποράκου.

 
Η Μόνα Λίσα σαν πρόβλημα περιπλανώμενου εμποράκου με 100.000 πόλεις/σημεία, από tsp.gatech.edu.

Του Σίμου Γερασιμίδη

Δείτε το Β’ μέρος >>

Αναφορές:
1. http://coloring-page.net
2. http://wikipedia.com
3. http://voyage.gc.ca/.
4. http://www.tsp.gatech.edu/history/index.html